Anti Mainstream: April 2016

Judul yang kami ambil untuk materi UTS ini adalah perbedaan penggunaan bahan bakar untuk sepeda motor di kota dan di desa. Semua data bersumber dari bps.go.id, dan kami mengambil Indikator perilaku peduli lingkungan hidup 2014 (Hasil Survei sosial ekonomi nasional 2014, modul ketahanan sosial) sebagai referensi kami.

Jadi dari data tersebut kami akan mencari korelasinya, dengan hipotesa seperti berikut :

h0 : tidak ada perbedaan antara penggunanaan bahan bakar untuk sepeda motor di kota dan di desa (korelasi kuat).

h1 : ada perbedaan antara penggunanaan bahan bakar untuk sepeda motor di kota dan di desa (korelasi tidak ada).

*maksud tidak ada perbedaan adalah di desa maupun di kota sama saja dalam penggunaan bahan bakar

Dari hasil pengolahan data didapatkan hasil sebagai berikut :

Berikut Kami sediakan File program untuk dipelajari dan di download :

1. File SPSS

- Korelasi

- Korelasi2

2. File Video

- Korelasi

- Korelasi2

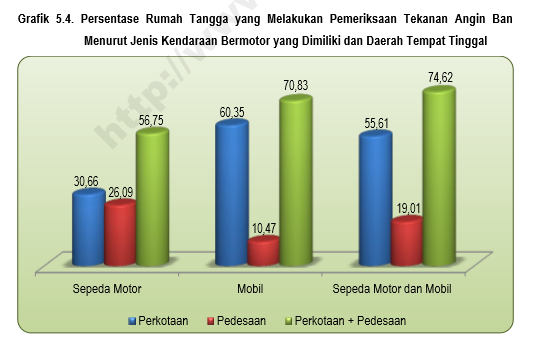
Pada postingan kali ini, saya akan membahas beberapa hal terkait regresi berganda yaitu :

Hubungan linear lebih dari dua variabel
Taksiran atau pendugaan tentang koefisien regresi parsial
Pengujian hipotesis koefisien regresi parsial
Hubungan antara koefisen regresi parsial dan koefisen korelasi parsial
Analisis Varians dalam regresi linear dan peramalan dengan menggunakan regresi linear berganda
Pendugaan atau ramalan dengan menggunakan regresi linear berganda

Semuanya telah kami bahas baik dalam bentuk spss, C++, dan matlab yang disajikan dalam bentuk video tutorial yang interaktif.

Kelompok 20 Fauzan pramulia jilid 2

Pada postingan kali ini, saya akan membahas beberapa hal terkait regresi berganda yaitu :

Hubungan linear lebih dari dua variabel
Taksiran atau pendugaan tentang koefisien regresi parsial
Pengujian hipotesis koefisien regresi parsial
Hubungan antara koefisen regresi parsial dan koefisen korelasi parsial
Analisis Varians dalam regresi linear dan peramalan dengan menggunakan regresi linear berganda
Pendugaan atau ramalan dengan menggunakan regresi linear berganda

Semuanya telah kami bahas baik dalam bentuk spss, C++, dan matlab yang disajikan dalam bentuk video tutorial yang interaktif.

REGRESI BERGANDA

Hubungan linear lebih dari dua variabel

Untuk memperkirakan atau meramalkan nialai variabel Y, akan lebih baik apabila kita ikut memperhitungkan variabel variabel lain yang ikut mempengaruhi Y. Dengan demikian kita mempunyai hubungan antara satu variabel tidak bebas (dependent variabel) Y dengan beberapa variabel lain yang bebas (independent variabel) X_(1, ) X_2, ....., X_k

Misalnya Y= hasil penjualan, akan dipengaruhi oleh daya beli (X_1), harga (X_2), dan lain sebagainya; Y = produksi padi, akan dipengaruhi oleh X_1 = bibit, X_2 = pupuk, X_3 = curah hujan, X_4 = luas sawah dan lain sebagainya.

Koefisien Determinasi Berganda dan Koefisien Korelasi Parsial

Didalam subbab ini, hanya akan dibahas hubungan berganda antara 3 variabel, yaitu Y (variabel tidak bebas) dan dua variabel bebas X_1 dan X_2. Bentuk persamaan regresi perkiraan adalah Y = b_0 + b_1 X_1 + b_2 X_2.

Misalnya, Y = produksi padi, maka X_1 = pupuk yang digunakan dan X_2 = luas sawah, Y = hasil penjualan, maka X_1 = biaya iklan, X_2 = pendapatan. Untuk memperoleh nilai b_0, b_1 dan b_2 Sebagai penduga dari B_0, B_1 dan B_2, diperlukan data sampel. Misalnya ada hasil n hasil observasi sebagai berikut :

Koefisien Korelasi Parsial

MASALAH REGRASI LAINNYA

di dalam model regresi yang sudah dibicarakan sebelumnya, dianggap bahwa kesalahan penggangu

merupakan variabel acak yang bebas.

banyak kesukaran akan dialami pada analisis ekonomi, apabila asumsi tersebut tidak berlaku. Hal-hal dimana kelahan observasi tersebut berkolerasi satu sama lain, atau terjadi otokorelasi

Semuanya telah kami bahas baik dalam bentuk spss, C++, dan matlab yang disajikan dalam bentuk video tutorial yang interaktif.

Anti Mainstream

Laman

Selasa, 26 April 2016

UTS Kelompok 20 Fauzan Pramulia dan Vedo Alfarizi

Senin, 25 April 2016

UAS Kelompok 20 Fauzan Pramulia dan Vedo Alfarizi

Presentasi Kelompok 20 Fauzan Pramulia Jilid 2

Kelompok 20 Fauzan pramulia jilid 2

Visitor

Sposnsor

Sponsors